
| |
||
| |
||
 |
||
| |
|
|
Overview
|
Brass players can make musical sounds with just their lips, as you'll hear in the sound files below. This is one of the first things a brass player learns: you close your mouth, pull your lips back in a strange smile, and blow. The result may be anywhere between a low pitched 'raspberry' or a high pitched musical note, depending on the tension and the geometry of your lips (how hard you pull them backwards in that smile), how hard you blow and other parameters. (It's easier to play with an instrument connected, but you can play with only a mouthpiece, or even without that: the resonator is not strictly necessary.)
How does that work? Here is a considerably simplified description. Lips are springy: if you form your embouchure then pull your top lip forward (horizontally) with your fingers and let it go, it will spring back to its original position. If you pull the top lip up (vertically), it will spring down. So lips are springy in (at least) two directions. Lips also have mass, and a mass and a spring together can oscillate. Lip vibrations are more complicated than the linear mass-and-spring oscillator that one finds in introductory physics books. (Nevertheless, simple models with one degree of freedom show some of the important features in lip-bore interactions.) First, let's think of two different oscillations here: the vertical and the horizontal motion, with their different springs. What happens here is a cycle of horizontal and vertical motion that converts the DC flow of air at high pressure out of your lungs into an oscillating air pressure and air current. (When an instrument is present, this leads to a standing sound wave in the bore of the instrument, and the fluctuating pressure in the mouthpiece can help move the lips, as we'll see below.)
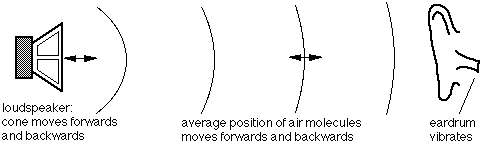
The simplified schematic shown below represents a cross section of the lips, viewed from the side. Consider state (1), with the lips closed. At this point, the air pressure in your mouth is (and has been) higher than that in the mouthpiece: this has accelerated the lips forwards, so in (1) they are moving forwards. A short time later (2), they are open and air flows out between the lips (2-3-4), as indicated by the arrow. The lips then close (4 to 1) and the cycle then repeats.
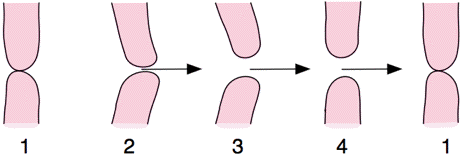
The phase of the motion is important to the energetics of oscillation. The pressure in the mouth is always at least a little higher than in the mouthpiece (much higher when the lips are closed — see below). The pressure between the lips is approximately the same as that in the mouthpiece (though this depends on the downstream turbulence). This means that the pressure difference can do work on the lips around a cycle. The lips move forward (picture 1 to 2) while closed or only slightly open; they retract (3 to 4) while open. So the volume swept in the horizontal direction is larger going foward than back. Because the pressure between the lips is low, this means that the pressure drop across the lips can do positive work on the lips around a complete cycle. In our measurements, this 'sweeping work' done around one cycle is comparable with the maximum kinetic energy of the lips and so it can replace the energy lost in the lip collisions.
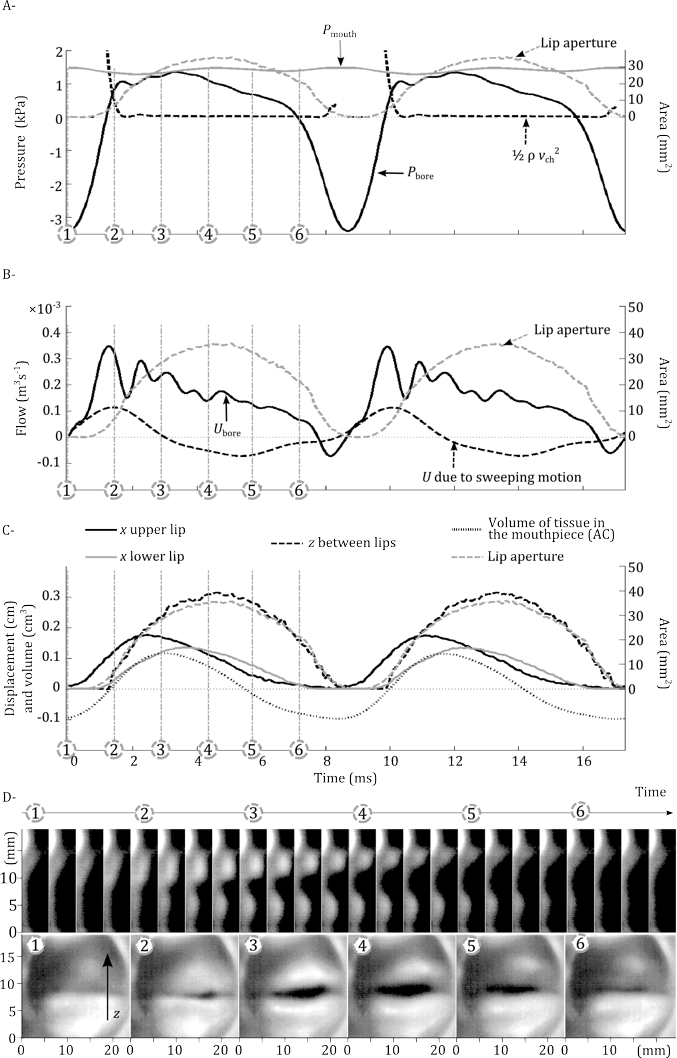
On the main graphs, the numbers 1-6 correspond to numbered frames from the high speed video side and front views shown in the two bottom lines. The trombonist plays a relatively low note: Bb2. For reference, each graph shows the area of the lip aperture as a function of time. The top graph shows the mouth pressure, the mouthpiece pressure, and the Bernoulli term (ρv2/2, the pressure reduction due to the moving air between the lips, where ρ is the density of the air and v its speed). The large pulse of negative pressure in the mouthpiece (time 1) accelerates the lips forwards. The middle graph shows the total flow of air into the mouthpiece (dark continuous line) and the component of flow due to the sweeping motion of the lips (positive when the are moving forward into the mouthpiece). The bottom graph shows the forward or x motion of the lips, the vertical separation z between them and the fluctuating volume of lip inside the mouthpiece. See this scientific paper for a more detailed explanation.
The explanations above are simplified. We have mentioned the different phases of the motion of the lips (forward motion leads the verical motion). Also very important is the phase of the air flow (out of the mouth and into the instrument) and the phases of the pressure in the mouth and the mouthpiece. In normal playing, the flow out of the mouth is a little ahead in phase of the pressure in the mouthpiece (however, players can vary this relatively easily). We discuss these (and give extended versions of the figure above) in this paper. (Another complication is that the channel between the lips may change shape during a vibration. In one reported mode of vibration the back (teeth side) of the lip channel has a bigger cross section than the front while the lips are opening and smaller while they are shutting. This can be modelled with two masses and two vertical springs in each lip, the masses vibrating with different phases.)
Playing frequency and pitch. The more tension you apply to your lips (the harder you pull your lips backwards in a smile), the more quickly they spring back into position. If the whole cycle of vibration takes a time T (called the period), then there are {(one second)/T} cycles in a second. So the frequency f, in cycles per second, is just f = 1/T. All else equal, high lip tension gives high frequency and so high pitch. In the sound files above (play them again), the lip tension is increased and decreased smoothly. Without the instrument, you can easily vary f smoothly.
This frequency of the lip vibration is the fundamental frequency of the note. For a high trumpet note, the lips may vibrate at more than 1000 vibrations per second. This is fast, but remember that the muscles are not contracting at that rate: the muscles in the brass player's lips exert almost constant tension, and it is the elastic and aerodynamic forces on the lips that produce the vibration.
The film clip below was made using a transparent pipe played as a didjeridu, at a frequency of about 80 Hz. On the left you see a high speed video of the lips, on the right schlieren images of the air jet from the lips. More details on our didjeridu (yidaki) site.
Adding (only) a mouthpiece changes the situation: the mouthpiece rim reduces the amount of the lips that move, and it allows the pressure outside the lips to be a little different from atmospheric, especially at high frequency. We'll discuss mouthpieces in detail later, but for now here is a sketch of the lips and a horn mouthpiece. Many players position the mouthpiece asymmetrically, so that it covers more of the upper lip than the lower lip, as is shown here. More about lip position below.
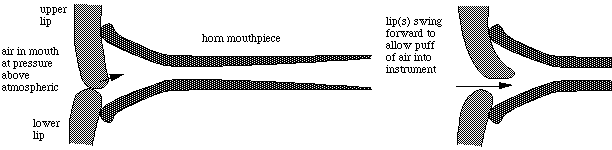
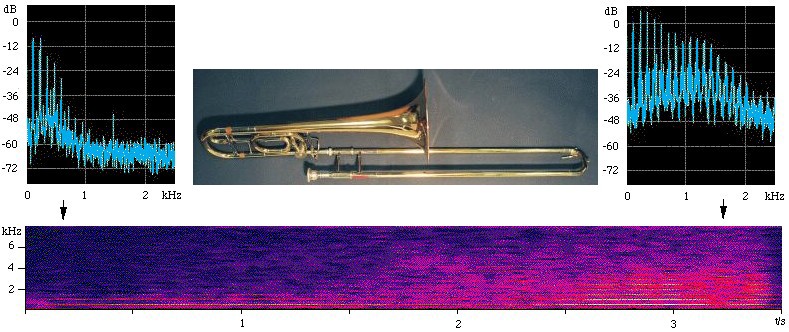
In this figure, the two upper figures are spectra that were taken over the first and last 0.3 seconds of the sound file. The spectrogram (lower figure) shows time on the x axis, frequency on the vertical axis, and sound level (on a decibel scale) in false colour (blue is weak, red is strong). In the spectra, note the harmonics, which appear as equally spaced components (vertical lines). In the spectrogram, the harmonics appear as horizontal lines. Note that the pitch doesn't change, so the frequencies of the spectral lines are constant. However the power of every harmonic increases with time, so the sound becomes louder. The higher harmonics increase more than do the lower, which makes the timbre 'brassier' or brighter, and also makes it louder. (To re-emphasise our point about loudness: over this crescendo, the fundamental increases by only 8 dB, but the ninth and some higher harmonics — in the sensitive range of your ear — increase by more than 45 dB.)
An interesting point about loudness in brass instruments. In acoustics, we are usually interested in cases in which the amplitude of the sound pressure wave is only a tiny fraction of atmospheric pressure. Consequently, the medium (air) behaves linearly for such waves, which simplifies the mathematics considerably. For example, a sound of 120 dB is painfully loud, but it corresponds to a sound pressure of only 20 Pa, or 0.0002 atmospheres. At the position where the viola player is complaining about the pain in her ears from the trumpets behind her, the sound level is probably (hopefully!) still below 120 dB.
However, inside the narrow bore of the instrument, the sound pressure is much higher, for two reasons. First, it is concentrated in a small cross sectional area, instead of spread out over a much larger area outside the instrument. Second, most of the sound inside the instrument is reflected at the ends to provide the standing waves we have discussed above. So the pressure inside a brass instrument can be a substantial fraction of atmospheric pressure, and so the medium can behave in a non-linear way. This can produce a shock wave in the instrument, which results not only in the conversion of power from low frequency to high, but also in the production of frequencies that are not harmonic. This phenomenon was analysed formally by Mico Hirschberg and colleagues (1996, JASA, 99, 1754-58). It is stronger in instruments with long, narrow sections of bore (trumpets and trombones) than in others (flugelhorn or tuba). Some scientists associate the onset of the shock wave with what some brass players refer to as cuivré or the sizzle point. (Here is a video showing the emergence of the shock wave.)
While talking about decibels, we should mention that spectra are usually shown on a decibel scale. (See What is a decibel?) This means that one notices easily on the spectrum a harmonic that is say 20 dB weaker than the fundamental, even though it has 10 times less pressure and 100 times less power. What is important is that your ear notices it too, because of the frequency dependence referred to above. However, it is much more difficult to notice the presence of harmonics if you look at the waveform: for this reason, an oscilloscope is only of limited use.
The shape of the pipe varies widely among instruments. For the modern instruments, there is a section of tubing with constant diameter (this includes the slide of the trombone and the section containing the valves of other instruments). On the upstream end is a mouthpiece, which has a little cup-shaped section and a constriction. At the other is a flaring section ending in a bell (the flare is longer in a tuba than in a trombone, and longer in a flugel horn than in a trumpet). In the diagram below, the vertical and horizontal scales are different: the ratio of width to length has been greatly exaggerated to show the variation in diameter more clearly.

|
The shapes whose acoustical properties are easiest to understand are the simple conical bore (rather like the cornetto) or the cylinder (rather like the didjeridu). We devote a whole page to the acoustics and harmonics of cylindrical and conical bores, open and closed because the oboe, saxophone and bassoon are closed, approximately conical bores, the clarinet is nearly a closed cylindrical bore and the flute is well approximated as an open cylinder. If you are interested in what finger holes do on the older lip reeds, go to the section on tone holes on saxophones, because a saxophone can be considered approximately as just an ophicleide with a clarinet mouthpiece.
In fact, we shall see that several of the resonances (often called 'harmonics' by brass players) of the modern brass instruments are not very different from those of a cone. Exceptions are the fundamental or pedal note, and the very highest notes. To understand why, we shall 'build up' a brass instrument, starting with a simple piece of pipe.
In these cases, the lips and the pipe were in a sense cooperating to form the vibration that gives rise to the sound. The lips may have their own natural vibrating frequency, which the player can control with lip tension. The pipe has also its own resonances and natural frequencies, which are due to standing waves. We have a page devoted to pipes and harmonics, and another on standing waves. We briefly review the results here.
At the far end, the pipe is open to the air, so the pressure there must be close to atmospheric at all times: in other words, the varying part of the pressure (what we call the acoustic pressure) is relatively small. We call this a pressure node. At the other end, the pipe is sealed from the atmosphere by the player's lips, and the pressure can vary maximally as the lips open (admitting a pulse of high pressure air from the mouth) and close: at this end we have a pressure antinode. If we look for the simple waves that satisfy these constraints – maximum at the mouthpiece, minimum at the bell – we obtain the set shown in continuous lines below.
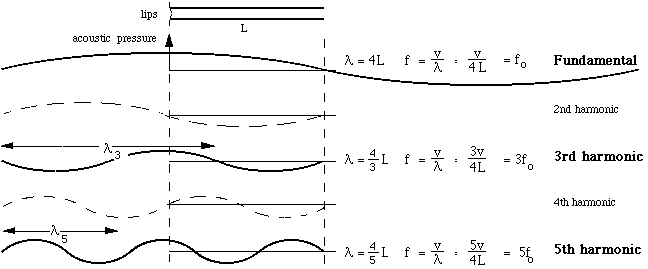
These frequencies are in the ratio 1:3:5:7 etc. They constitute the odd members of the harmonic series, and they are what we heard in the sound file above. The even harmonics (dashed in the figure) don't fit the conditions in a closed, cylindrical pipe because they have a node at the mouthpiece. (More detail in Open vs closed pipes.)
(Before we go further, we should note that the resonances of a simple pipe are only exactly harmonic if the pipe is very thin. As the pipe diameter increases, the higher resonances are successively flatter. This is quite noticeable in a cylindrical didjeridu.)
The short waves, on the other hand, are better able to travel into the rapidly widening bell. The further they go into the bell, the easier it is for them to escape into the outside air. So the higher frequency waves are more efficiently radiated as sound outside the instrument. This is a characteristic of the sound of brass instruments: the bell radiates several of the higher harmonics well. This also makes brass instruments loud, because these strongly radiated moderately high frequencies begin to fall into the range where our ears are most sensitive. To hear the effect of the flare and bell, listen to the sound files below. Notice how the bell raises the pitches of the first three resonances, and also brings them closer together. We'll discuss that in detail below. We still haven't added a mouthpiece, but notice that the bell has made it sound more like a brass instrument.
 A cylindrical pipe, 110 cm long. (No mouthpiece.)
A cylindrical pipe, 110 cm long. (No mouthpiece.)
![]()
 A 110 cm pipe, including flare and bell. (No mouthpiece.)
A 110 cm pipe, including flare and bell. (No mouthpiece.)
The bell also works in the other direction. The bell has another interesting effect: the pressure of waves coming from outside the instrument can be considerably increased as they enter the instrument through the bell. (It works in both directions, like an ear trumpet and a gramophone horn.) A practical consequence is that timpani strokes can disrupt playing if the horns are seated too close to the timpani. More details about this effect.
Finally, let's add a mouthpiece. Now we can play the normal harmonic series (see standing waves to revise about harmonics), including the notes used for bugle calls. We'll see why in the next section.


When placed against the player's lips, the enclosed volume is sealed at one end by the lips, and has the constricted part of the pipe at the other end. You might imagine it as a tiny bottle, with your lips at the base of the bottle, and the constriction representing the neck of the bottle. Now, just as the bottle has a resonance that you can excite by blowing over the top, the mouthpiece has a resonance that you can excite by slapping the wide end to close against the palm of your hand. When shopping for mouthpieces, brass players sometimes do this to compare what they call the 'pop tone'. It is much easier to hear the pitch if you compare two: say a trumpet and a trombone mouthpiece. As you might expect, the larger the volume (all else equal), the lower the pitch of the pop tone. Reducing the diameter of the constriction also lowers the pop tone. This is an example of a Helmholtz resonator, whose frequency depends on the enclosed volume and the geometry of the constriction. THis resonance is changed when it is installed on the instrument, but it has an important effect on the resonances and, as we shall see, on the impedance spectrum.
When shopping for mouthpieces, brass players sometimes do this to compare what they call the 'pop tone'. It is much easier to hear the pitch if you compare two: say a trumpet and a trombone mouthpiece. As you might expect, the larger the volume (all else equal), the lower the pitch of the pop tone. Reducing the diameter of the constriction also lowers the pop tone. This is an example of a Helmholtz resonator, whose frequency depends on the enclosed volume and the geometry of the constriction. THis resonance is changed when it is installed on the instrument, but it has an important effect on the resonances and, as we shall see, on the impedance spectrum.The volume of the air in the mouthpiece depends a little on how far your lips protrude into it, and that varies among people. If your lips protrude further in, then it's tempting to suggest that you should try a larger volume mouthpiece, and vice versa. However, I know of no formal study of this.
The mouthpiece does a few things. First, it allows you to connect the pipe to a comfortably large section of lips. Then there are the acoustic effects of the enclosed volume and constriction. One effect is to lower the frequency of the very highest resonances (roughly speaking: those above the pop tone). So in this regard it opposes the effect of the flare and bell, which tend to raise all the resonances. Another is to strengthen some of the resonances. We'll return to this when we discuss the spectrum of brass instruments. But first, let's look at the combined effect of the mouthpiece, pipe, flare and bell.
Resonances and pedal notes.In this diagram we show at left the resonances of a simple cylindrical pipe, like a very narrow didjeridu. It is 130 cm long, and its lowest note is C2. As a closed, cylindrical pipe, its resonances are the odd harmonics of its fundamental frequency F (careful: here F is a symbol for frequency, not the note above E). We now add a mouthpiece at one end, and at the other we replace a long section of cylindrical pipe with a flare and a bell, to obtain a bore much like that of a C trumpet. The resonances all rise in frequency and pitch (flare and bell effect), although the upper resonances rise proportionately less (flare, bell and mouthpiece effects together).The shape of the trumpet is so designed so that the second and all higher resonances have risen so that they have frequencies in the ratios 2:3:4:5 etc. In other words, the resonances are a complete harmonic series, except for the fundamental. The lowest resonance of the trumpet is not a member of this series. Further, it is weak and rather difficult to play (try playing a note below the bass clef on a Bb trumpet). Instead, however, good players can play the pedal note, whose fundamental frequency does not correspond to a resonance of the instrument! Further, the spectrum of a pedal note has hardly any power at the fundamental frequency. (We show this quantitatively below in Frequency response and acoustic impedance.) What happens in the pedal note is that the higher resonances (2f, 3f, 4f etc) combine to help the lips establish a nonlinear vibration at the frequency of the missing fundamental f. (Technically, this is the process that physicists and engineers call mode locking, and is an effect characteristic of nonlinear oscillators. When oscillations at two frequencies f1 and f2 are input to an non-linear system, they produce what we call sum and difference terms: vibration components with a range of frequencies including f1 + f2 and f1 − f2. In the pedal note vibration, there are lots of vibration components whose difference is f: any two adjacent resonances have that difference.)
|
|
Twe little exercises. The frequency equals the wave speed divided by the wavelength (we write f = c/λ), so the longest wave corresponds to the lowest note on the instrument. (See standard note names, and remember that some brass are transposing instruments, so that the written C4 is actually Bb3 for a trumpet in Bb.) You might want to measure the length of tubing in your instrument (not including the little tubes of the valves for the moment), take v = 345 m/s for sound in warm, moist air, and calculate the expected frequencies of the 2nd, 3rd and 4th resonances. Do you get a better answer if you pretend it is a cylinder or a cone? (To convert notes to frequency, see notes.) For instance, with no valves depressed on a trumpet, you can play the lowest note: (written) C4. You may also be able to play the pedal note at (written) C3 (but remember that there is no resonance at this frequency). (If you're a trombonist, shift these instructions down an octave.)
If you have a trombone, find a note (like D4, two spaces above the bass clef) that you can play with the slide in two different positions (first and fourth for this case). Using 345 m/s for the speed of sound, calculate the wavelength (the nominal frequency of an equally tempered for D4 is 294 Hz.) Measure the distance between these two positions, calculate the change in the instrument length and compare with a wavelength. Is this what you would expect for a cylindrical tube?
| By the way, you can also play this harmonic series on a string, because strings also have the complete harmonic series. You could also play the first several of them on a bass flute (whose lowest note is C3), because a flute (open cylindrical pipe) has a complete harmonic series, or an octave higher on a normal flute. |
The natural trumpet and natural horn use this. The natural or baroque trumpet came in a variety of tunings, but was usually rather longer than the modern trumpet. This transposes the harmonic series down, which brings the high harmonics into a more easily playable range. Here is Paul Plunkett, professor of trumpet at the Conservatorium of Winterthur, playing the Prince of Denmark March on a baroque trumpet in D, whose harmonic series we see here, followed by the first two bars of the march.
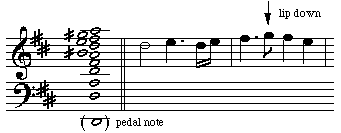
|
Many of the intervals between pairs of the higher harmonics are, shall we say, less usual harmonies. In our example, the seventh lies about half way between A and A# (note the half sharp symbol on this and the preceding graphic) in the equal tempered scale. Similarly, the eleventh harmonic is approximately a half sharp fourth on the scale. On baroque trumpets and horns, the player adjusts the intonation to bring these 'out of tune' notes into more familiar scales, as Paul Plunkett does in the example above.
![]() The opening bars of Britten's Serenade
for Tenor, Horn and Strings.
The opening bars of Britten's Serenade
for Tenor, Horn and Strings.
However, the resonances of the bore are, for low frequencies at least, narrower in frequency and 'stronger' than those of the lips: this allows the resonances of the bore to 'take control'. To oversimplify somewhat, a lip reed instrument usually plays very close to a strong bore resonance; which one is determined largely by the lips. (If you are interested, we have a technical paper on the physics of lip mechanics.)
The 'taking control' is never complete, however: it is always a compromise. So the player can adjust the pitch of a note by changing lip tension, even if the frequency of the resonance of the instrument does not change. Trombonists may play vibrato by moving the slide slightly, but players of other brass instruments do it by 'lipping' or rocking the instrument.
Finally, we should mention here that the player's lips actually interact with two resonators: those of the bore of the instrument, and those of the vocal tract. The instrument's resonances are usually much 'stronger' than those of the tract, but the latter are not negligible. This is an area of great interest to us, and we studied it first on the didjeridu, where it is most important. We have also studied it on trombone and trumpet, and have published some of the results: see below.
The three individual spectra are for the lowest note played herre (written C4 = sounding Bb3), and the notes one and two octaves higher. The fourth spectrum is the average over time for the whole scale. Why do the spectra have their characteristic shapes?
In all wind instruments, the higher frequency harmonics are relatively inefficient because they lose energy in viscous and thermal losses – a sort of friction with the walls, so this explains (in part) the shape at high frequencies. However, for brass instruments, the radiated power sometimes increases with frequency over the low part of the range, as here. This means that one tends to get maximum radiation at a moderately high frequency (typically around several hundred Hz, although it has a different value in each lip reed instrument), and less power at lower and higher frequencies. Further, the enclosed air in the mouthpiece and the constriction beyond it also tend to drive the lips most efficiently near this frequency, further contributing to the peak. (We should add that this is complicated by the fact that the standing wave in the bore also affects the lip vibration, so a strong standing wave in the bore could affect the component of the lip motion at that frequency. I don't know of a formal study of this.)
Remember, however, that the spectrum depends strongly on how loudly you play. The larger the vibration of the lips, the more non-linear the vibration, so the more strong high harmonics present in the sound. (See Playing softly and loudly above.) Indeed, if a trombone plays very loudly, the acoustic pressure in that relatively narrow pipe ceases to be tiny in comparison with atmospheric pressure. When this happens, the linear wave equation for air no longer applies, and the spectrum itself begins to contain non-harmonic elements. You'll recognise this harsh, almost unmusical sound if you know a loud trombonist.
One simple way of changing the spectrum of a brass instrument is to modify the performance of the bell with a mute, which is our next topic.
| On the right are the time-averaged spectra of the two sections of the sound file. Note that the mute attenuates the lower frequency components, but produces a formant at about 1 kHz. (Because several different notes are played, the harmonic structure of the individual notes is obscured.) |
|
Almost anything that occludes a substantial fraction of the bell will act as a mute. The real difficulty in designing a mute is to arrange the reflections at the bell so that, even though the resonances are shifted, the tuning of the playing frequencies is little affected. (There's a paper including this subtle problem in this magazine.) One exception is the hand stopping of the french horn. In this case, not only is the timbre changed, but the pitch may be altered by about a semitone or so.
The trombone of course solves this problem by having a continually variable length using the slide. The other brass instruments use rotary or piston valves.
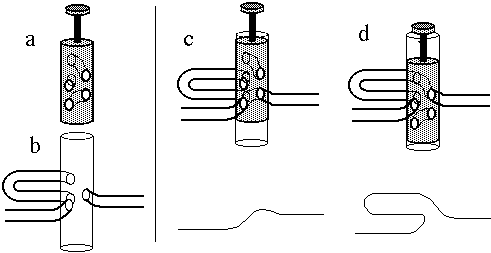

|
How long should the second valve pipe be? To make the calculation simple, let's imagine that we are designing valves to make a narrow bore, chromatic didjeridu (ie we are going to add valves to a simple cylindrical pipe), whose natural length is 100.0 cm. If the second valve lowers the pitch of the natural pipe by an equal tempered semitone, then it must decrease the frequency by 5.9% and thus increase the effective length of the instrument by 5.9 cm. So the difference in frequency between − − − and − 2 − is now 5.9%.
However, if we are to use the fingering scheme above, we also want the second valve to lower the pitch from 5 to 6 semitones below the natural frequency. Suppose that the first and third valves do lower it by 5 equal tempered, in other words they decrease the pitch by 33.5% and so must together add a length of 33.5 cm. So fingering 1 − 3 has pipe of length 133.5 cm. If we add our 5.9 cm, we increase this to 139.4 cm. This is an increase of 5.9 cm/133.5 cm, which is only 4.4%, which is only three quarters of an equal tempered semitone. The standard way to fix this problem is to use a slide. The problem is worst when the third valve is used, so many trumpets have a slide on the added pipe for this valve that allows the player to increase the length to solve problems such the one we have just discussed. On the larger instruments, this would require a lot of work for the finger operating that slide, so one or more extra valves is added.


Scaling up. The Italian for trumpet is tromba, and the suffix for 'big' is -one. So a trombone is a etymologically a big trumpet. We have seen that the method of changing the length is different for the two but, apart from that, they are not very different from being scale models, at least in the acoustical sense. The tenor trombone is twice as long as the Bb trumpet (though less than twice the cross sectional area).
This scaling allows us to do an interesting demonstration. In the first pair of sound files, we hear the Prince of Denmark march played again by Paul Plunkett. So that we do not get the acoustical clues from the slide, he is playing it as though it were a very low pitched baroque trumpet: he plays using the high harmonics and does not use the slide. (He also plays slowly, so that we can later increase the playback speed.)
The next sound files have the same recording, but played back at twice the speed. Of course the pitch is an octave higher, and so are all the harmonics, so we might expect it to sound like a pipe of half the length.Of course we have not made a complete scale model: the player's lips are not scaled here. But let's see how different the 'scaled trombone' is from a trumpet. The modern Bb trumpet is half as long as a tenor trombone. Here Paul plays the same tune on a modern trumpet (again, no valves: starting on the 8th harmonic and just using the lips). Listen to this and decide how different or similar they sound. Different bore shapes. The trumpet, trombone and french horn have relatively long lengths of narrow cylindrical pipe, and a relatively short flared section. Another family of brass instruments have much longer flares and shorter cylindrical pipes. These include the bugle, the cornet, the euphonium and the tuba.
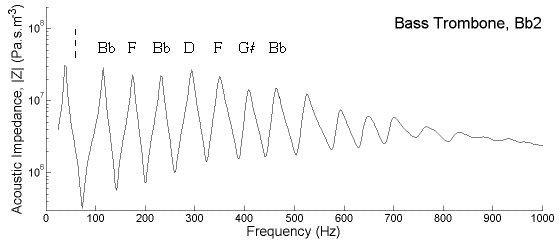
Acousticians characterise many of the properties of musical instruments by their acoustic impedance spectrum. This is a measure of how much sound pressure is generated by a sound wave of a given frequency at the mouthpiece of the instrument. For a brass instrument, the lips require a strong pressure signal to help the lips vibrate, so brass instruments tend to play notes near the peaks in the graph of acoustic impedance as a function of frequency. The graph below (measured by Jer Ming Chen, a PhD student in our lab) shows such a graph for a bass trombone, with the slide in and the trigger not depressed. The lowest normal note for this position is Bb2 at about 116 Hz – the second peak on the graph.
This graph shows several of the features discussed above. Of the first several resonances, all but the first form a nearly harmonic series – they are nearly equally spaced in frequency. The notes that they play are labelled on the graph. (The first is far too flat, as explained above in Resonances and pedal notes, and is difficult to play. It does not correspond to the pedal note, which is played at about Bb1, half the frequency of the second peak and indicated by a dotted line.) Again, the seventh harmonic corresponds to a note absent in standard Western scales, hence the half sharp symbol. Note too that the resonances become successively weaker at high frequency. This is partly because the bell effectively radiates high frequencies rather than reflecting them, but a larger effect is due to the frequency response of the mouthpiece as discussed above. The resonances disappear altogether at high frequency, and the trombone begins to function as a megaphone, rather than a resonator, above about 700 or 800 Hz.
The way in which these measurements were made is given in this paper. More recent impedance measurements of Z(f) by Henri Boutin are available here: Download file and graph.
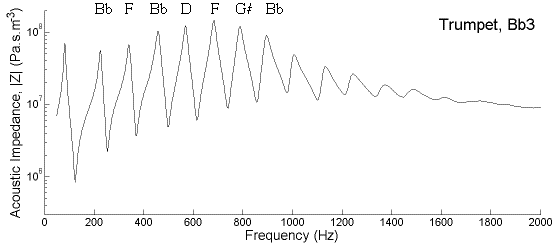
Below, we compare the impedance curves for a Bb bass trombone (first position, valve not depressed), a Bb trumpet (no valves depressed) and a horn in the open Bb and F states (no finger valves depressed). The trumpet is shown on a frequency scale that is twice that of all the others. This facilitates comparison with the trombone, and shows that the trumpet is rather like a one-half scale model of the trombone. (Etymologically, the reverse is true: trombone means big trumpet.) The narrower bore and especially the narrower mouthpiece constriction in the trumpet and horn give them, overall, higher values of impedance than those of the trombone. (These impedance spectra were made by Jer Ming Chen, a student in our lab, using a technique described in this scientific paper. If you want to cite them, the reference is: Chen, J.M. (2009) Vocal Tract Interactions in Woodwind Performance, PhD thesis, UNSW, Sydney.)
The third graph shows Z(f) for a horn playing open Bb. As with the trombone and trumpet, the bell radiates high frequencies well, rather than reflecting them, so the resonances become weak at high frequencies. However, the horn is played with the hand positioned in the bell. This increases reflection at high frequency and the stronger peaks in Z make high notes easier to play. The hand also lowers the frequencies of each resonance. Before the introduction of valves, and occasionally still, different extents of hand stopping were used to vary the pitch.
Illustration of bell effect. The insertion of the hand reduces the good radiation of the bell: this gives the player a few more clear high resonances but reduces the loudness and brightness of the sound. So, when the composer asks for 'pavillons en l'air' (bells up), the sound is loud and bright, please don't write high passages with this instruction!
Most horns are double horns: the player has a valve for the thumb that introduces extra tubing to convert between a Bb horn (lowest playable resonance Bb2 and pedal Bb1, like the trombone) and an F horn (lowest playable resonance F2 and pedal F1, like the bass trombone with the valve depressed.) The horn also has three keys, each of which is connected to two valves, one in the F and one in the Bb horn. As usual, the finger keys add appropriate lengths of tubing to lower the pitch by about 2, 1 and 3 semitones respectively.
Horns are occasionally required to play pitches above 500 Hz. The increase sharpness of the impedance peaks provided by the hand make this easier to do. Comparing the last two curves, we can see why horn players often prefer to play the Bb horn for the high range. The player must select which impedance peak will determine the note by adjusting his/her embouchure. On the Bb horn, the peaks are further apart and one is less likely either to select the wrong one, or to crack a note by involving two neighbouring peaks. (Another interesting reason for cracked horn notes is here.)
Comparing the Z(f) curves with and without the hand in place shows clearly the compromise involved in the shape of the bell. A smoothly flaring bell radiates well and makes a bright, brassy sound. But the impedance peaks get weaker with incresing frequency, making it difficult to play high notes. (See the 'no hand' curve.) Putting the hand in the bell deforms the smooth shape of the air that conducts the sound. Reflections at the bell are stronger, so the high resonances are stronger and there are more of them. However, the bell radiates less well at high frequency, so it works less well as a megaphone, and the sound is darker and less loud.
Note again that the seventh and eleventh peaks are not very close to a note in the equal tempered scale, but are quite close to the natural harmonics of the pedal. We discussed this above in Intonation in the natural harmonic series.
As mentioned above, the player's lips are loaded by two resonators: downstream is the bore of the instrument, while upstream is the vocal tract. If we consider the longitudinal motion of the lips to be driven largely by the pressure difference between the mouth and the mouthpiece, the vocal tract is in series with the bore: their acoustic impedances just add up (This follows from the continuity of air flow. And remember, however, that the sum of complex numbers must include the phase). Further, in a simple model, the series combination is approximately in parallel with the passive impedance of the lips themselves. Because the impedance of the bore is very large at resonant frequencies, one would expect that different vocal tract configurations have relatively small effects on a given playing regime. The graph below (from this paper) shows the frequency of notes 'played' by a simple mass-on-spring cantilever valve instead of lips. Downstream from the valve, there was a trombone. Upstream, there were two different geometries acting as artificial vocal tracts. The 'high tongue' configuration (with a constriction upstream from the valve) played a somewhat higher pitch for most slide positions. However, it also caused the register transition to occur at a higher pitch.
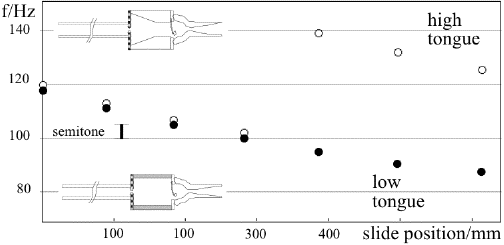
Players are aware that tongue placement and other changes in the mouth configuration affect the intonation and also the transition between registers, and these measurements on an artificial playing system support such observations (as do some experiments we've done with live players). The details of how this works are subtle and not yet understood.
Now, as we've seen above, the resonances peaks for brass instruments are very strong at low frequencies, but less strong at high frequencies. So, in a series combination, the vocal tract impedance becomes more significant for high pitches. Is it possible, we wondered, that trombone and trumpet players 'tune' the vocal tract to the desired note when they played in the high range? (We had previously demonstrated such an effect in the saxophone. Like the trumpet, the high register – called altissimo – has rather weak impedance peaks and these notes are therefore hard to play. On this page, we show how experienced saxophonists tune the resonances of the vocal tract to select these high notes, and in other techniques as well.)
In measurements of the impedance spectra in the mouths of trumpet players, we find that the peaks in impedance have magnitudes that are sometimes comparable with those of the higher resonances of the instruments. However, we saw no consistent tuning. The plots below (from this paper) show the acoustic impedance measured just inside the mouth of a trumpet player playing a medium and a reasonably high note. They show strong impedance peaks, but their frequencies are not related to those of the note being played. The same is true of trombone players: the peaks in the vocal tract impedance do not seem to be tuned to the notes being played.
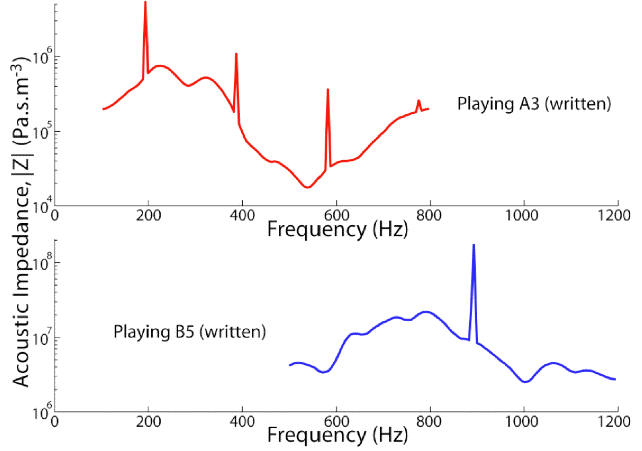
These results show that trumpet players play very high notes without tuning the vocal tract. Our studies showed no evidence of vocal resonance tuning on either trumpet or trombone. (See Chen et al (2012) and Boutin et al. (2015), both papers available on our publications list).
Brass players are able to vary the pitch substantially by 'lipping up and down', so that they play above and below (respectively) the resonance of the instrument. Their range of playing is approximately symmetrical about the resonance (in both magnitude and phase). However, their normal playing frequency is above the resonance so, with respect to normal pitch, they can lip down rather further than they can lip up. Above the resonance, air flow into the instrument is ahead in phase of the mouthpiece pressure (a compliant* load); below the resonance, pressure leads flow (inertive* load). The range over which players can do this can tell us something about the mechanics of the valve and we have studied it in this research paper. (* These terms explained here.)
A modern and relatively exotic performance technique asks players to sing into the instrument, while also playing a different note. In this situation, both the vocal folds and the lips are modulating the air flow. The result is not just two pitches, but a complicated set of frequencies corresponding to the sum and difference of the two frequencies, and others as well. For instance, playing the note C3 and singing G3 produces the low note C2. (Caution: sometimes this can cause discomfort to the vocal folds, because the relatively powerful pressure wave from the lips affects the vocal fold motion.) We discuss the physics involved in this research paper.
If you have questions, send them to us: we often post answers on our FAQ in Music Acoustics.
|
|
We shall continue to add to this site as we find time and as our research results are published: here are some papers from our publications list.
|
|
|
|