
'2. Sound waves can be used to illustrate many of the properties of waves that are utilised in communication technologies.'
'3. Recent technological developments have allowed greater use of waves in the electromagnetic spectrum that (sic) do not require a medium for propagation.'
'4. Many communication technologies use applications of reflection and refraction of electromagnetic waves.'
'5. Other properties of electromagnetic waves have potential for future communication technologies and data storage technologies.'
Using sound for a variety of wave examples. 'Sound waves can be used to illustrate many of the properties of waves that are utilised in communication technologies.'
Superposition in air
Radiation and travelling waves using sound

'Model the effect of different materials on the reflection and absorption of sound'

Relating these to the reflection and transmission coefficients is relatively simple algebra.
The material has a reflection coefficient that is less than one,
so the wave in the tube is the sum of a wave to the right and a smaller wave to the left. This can also be
written as the superposition (sum) of a standing wave and a wave to the right.
At the node of the standing wave, the amplitude (the minimum amplitude measured in the tube) equals the
amplitude of the travelling wave, i.e. the difference between the incident and reflected. At the antinode of
the standing wave, the amplitude is the sum of the incident and reflected.
Another tube cap, with a hole cut slightly smaller than the ID of the tube, could be used for a rough-and-
ready measurement of transmission with a microphone just outside. This requires baffles and is less
exact, but you could use the same gear.
Perhaps point it out through a window to minimise reflections onto your external mic, and then the wall
is part of your baffle. Most sound absorbant materials (like acoustic wool, carpet, fibreglass batts) absorb
much more in the kHz range than at low frequencies.
'Modelling the effects of different materials'. Perhaps this just means that one calculates what
different reflection and transmission coefficients would do to experiments like those above.
The effects in practical geometries, such as a room, involve many reflections and are thus rather
involved to model directly. Some acousticians are now doing that with huge ray-tracing calculations, but it is
rather time consuming for a high school project. Alternatively, one could go
straight to the reverberation time and Sabine's formula for it. Perhaps we should wait for
clarification on what is meant here
iv) For approximate results, one can use a narrow cylindrical tube and neglect end effects. A cylindrical dijeridu is readily made from 1-2 m of plastic conduit or plumbing pipe (smooth the end to be blown). A flute is approximately cylindrical. These can be used as the 'contextual' introduction to the exercise. (Our site on the acoustics of music has introductory material on a range of topics.)
Waves in slinky springs, water waves, ropes, strings. Displacement-time graphs
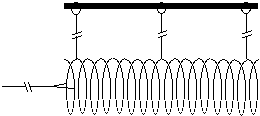
To reduce friction, suspend a slinky spring from a rod or from the ceiling by many threads of equal length threads (the longer the better for transverse waves in a nearly linear medium). This is a good way to allow a wave under low tension - and therefore speed: slow enough to see in detail. This method also shows reflection at a free end (or at least a big change in impedance) more easily than most media. The tension is controled by a thread at the end (~ free end for transverse wave), or by holding it firmly in a hand (~ fixed end). Slinkies can do transverse and longitudinal waves.
For water waves, if you have ripple tanks you will probably have gadgets that came with them, including vibrating bars for making beams of plane waves, and an instruction manual. In most cases, reflections are complicating (but interesting) factors. Remember that water waves have non-linear superposition when amplitude is not << depth - much loved by surfers, but a complication for superposition.
For ropes, rubber ropes (we use the flexible hose that your chemistry lab may use for the
Bunsen burners) have some advantages. One is that the length can be used to
control
the tension for reproducibility. Remember that ropes become non-linear media when the
displacement changes the tension (another advantage for rubber hose). Comparing stretched
ropes (observable motion at low tension and large mass) with musical string instruments
(which do the same thing too fast to see but fast enough to hear) is a useful teaching exercise.
Musical string instruments give convenient examples of standing waves in stretched
strings. These are very good for v = f*lamda (and for the effect of tension and string mass per unit
length on v). The electric guitar has a few ~ velocity transducers (pick-ups) built-in, and is a
familiar context for many students. A violin or bass bow is useful for exciting quasi continuous
standing waves. Harmonics are easier with a bow. (Get fibreglass ones for long life.) (For
more on harmonics, see our page strings).
A stroboscope, running at a frequency of n/m times that of the vibration (n and m
integers)
can be used to 'freeze' the motion of a periodic vibration e.g. a string in a combination of modes or a
drum head in a single mode*. If n = 1,
one image per cycle is seen. For neurological reasons it is unwise to look at a
strobe flashing at frequencies between 2 and 10 Hz.
* With the approximate exceptions of timpani and tabla, drum head mode frequencies are not
at rational fractions. However, the second lowest mode often lasts lower than the others.
"present and analyse displacement-time graphs for longitudinal and transverse wave
motion"
Direct experimental measurements are tricky, although one can sketch qualitative observations of
travelling and standing waves in a slinky or a rubber hose. The envelope of standing waves in guitar
strings can be seen and sketched. Velocity sensors (electric guitar pickups) and pressure sensors
(microphones) are much easier for measurements. Observing that the velocity has no DC component (the
string doesn't fly away and there is no wind), students can integrate the signal graphically, or you can
integrate it on an RC circuit to display displacement (from pressure to displacement is two
integrations).
Experiments with mobile phones
Turn on, wrap in Al foil and phone its number. Unwrap gradually. Demonstrates that
the good
conductor reflects EM waves. More importantly, it will also stop the phone ringing during class.
Light rays and geometrical optics
Laser diodes are a cheap way of getting a beam with low divergence (buy directly from an electronics or
hobby store for several $ including power supply: just add a battery. Or else buy assembled in laser
pointers). Can use to demonstrate ray representation of
fibre optics. They're also fun toys for a while and may seem more interesting than light boxes
(lamp source and cylindrical lens, gives a vertical plane of light). For plotting on paper, light boxes
are
immediately usable. A laser can also make a vertical plane of light by passing it through a
cylindrical
lens (axis horizontal). A suitable lens is a short section of plexiglass rod.
If you have light boxes, you probably also have a kit that goes with them: hemi-cylinders for
Snell's
law, 2D lenses for making optical instruments, cylindrical mirrors et hopefully cetera.
(By the way, cylinders of perspex make good model raindrops to show how rainbows form.)
Some notes about a guided investigation
This was one of the FAQ's and so I felt obliged to answer it: How to avoid the recipe lab exercise, but
still guide an investigation? I have almost zero
experience in
teaching high school students. Mosr readers of this document will have formal
qualifications and extensive experience in doing just that. Further, the labs that I have tried to run along
the lines tried here had relatively small
numbers
of students and taught different material. So it is with temerity that I offer some suggestions
about
trying to make an investigation less recipe based. I shall use Snell's law (not widely considered
exciting) as an example.
For me, the aim of teaching Snell's law is less important than teaching the method of careful
observation, improvement of measurement technique, generalisation and testing.
Some demonstrations to arouse interest, e.g. dismantle camera, use telescope/ microscope,
set fire to
paper using lens.
Some useful gear that is either
or both cheap and readily available.
A few web resources:
Some notes about the physics
of speech.
Some initial contextual question(s): Where do you find lenses? How does a lens work? Where would we
be
without
them? Who invented them? Who invented
Does light travel in straight lines? When?
When it doesn't, what happens? Explore and generalise qualitatively. Some questions: why does the
water look shallower? why does the surface of the water look silvery and strange to swimmers looking
up?
What are the consequences for vision? For natural phenomena? For optical instruments?
(higher
performance; mirages, distorted sun, green flash; spectacles, cameras, telescopes)
Paper work. What sort of relations might be involved? If you draw a diagram of wave fronts
incident
on a surface, what would light bending at an interface look like?
How can you obtain some relevant quantitative data using the gear we have here?
What makes the arrangement complicated? Are there ways you can reduce/eliminate the
complications or number of things to measure?
What will be the measurement errors? In particular, what is the largest measurement error
(protractor?
ruler? beam centre estimation?) and is there any way of making it smaller?
Are there some errors that can't be reduced and thus impose a limit to the precision of your
experiment? If so, can you reduce the other errors to this level?
Can you get a quantitative rule out of this? If different teams find different rules, what are the
cases
where they disagree? Can you test them to see which is supported experimentally? (If they
don't
disagree, can they be proved to be identical?
Suppose that you don't get Snell's law, or that you get a silly value for n, what then? Could the text
books be wrong? Could we have made an error in interpretation, or a systematic error? How badly does
Snell's law fit our data? How does the difference compare with the error?
Application: back to some of the examples, draw qualitative diagrams to explain operation.
How does
a lens or a mirage work? Do a quantitative ray diagram?
Opinions expressed in these notes are
mine and do not necessarily reflect the policy of the University of
New South Wales or of the School of Physics.