The Effect of the Soundpost on Violin Sound
J. E. McLennan
The sound output and the response of a violin were measured for three positions of the soundpost: no soundpost, inside and outside the treble foot of the bridge. The sound quality was assessed with Long Time Average Spectra that showed small differences. There were significant differences in the response plots, whether measured by a microphone in front of the top or a magnet/coil pickup on the bridge.
These results may be related to previous studies, in which the stiffness of the top plate at the bridge foot positions was measured for different soundpost positions. At the bass foot position, the stiffness did not change appreciably for these different soundpost positions. At the treble foot position, the stiffness was lower when the soundpost was placed inside the treble foot, and higher when it was placed outside.
Introduction
The bridge is mounted between the f-holes of the violin. If there were no mechanical support, the region of the top plate between the f-holes would be rather more compliant than the rest of the body. Two mechanical supports are present, however.
The bassbar is about 25 cm long, and is located under the bass foot of the bridge. It distributes some of the stress applied near the bass foot along the length of the bassbar, and thus to a large area of the front plate. The soundpost is typically located near the treble foot of the bridge: it transfers some of the stress applied by the treble foot to the back plate of the violin. In this typical set-up, the mechanical stiffnesses measured at the two feet are approximately equal.
Consider as a reference the stiffness at the bass foot when the soundpost is in a position a few mm behind the treble foot: a reasonably standard set-up. In a typical violin, as the soundpost is moved from a position between the feet to a position outside the treble foot [1], the stiffness at the treble foot increases from below that at the bass foot to a value above. This situation, however, varies among instruments and set-ups: the stiffnesses at the bridge feet depend on the top, back, bassbar and soundpost, as well as on the positions of the bridge and soundpost.
The position inside the bridge foot was considered unfavourable for producing a satisfactory sound quality and that outside was taken as favourable.
Three sound samples were taken using a violin called No 2 in my PhD thesis [1]. The violin was sealed but unvarnished, tuned to A440 and fitted with a 42 g chinrest. It was fitted with modern strings. The violin had well developed body modes, as well as A0, at the lower frequencies in the range of the violin as will be seen in the tap responses below. In the first sound sample, there was no soundpost. In the second and third, a soundpost was installed 10 mm inside the treble foot and then 5 mm outside the treble foot. With a soundpost in place at the treble foot of the bridge, the violin was 15% stiffer at the treble foot than at the bass foot.
Measurement of soundpost position
Figure 1 illustrates the geometry of the bridge/soundpost configuration. The bridge line is taken as a line between the inner notches in the soundholes as this was designed to be the “Stop” or “Diapason”. Since the rear face of the bridge is kept normal to the plane of the violin, the string notches on the top of the bridge are close to this position. In figure 1, the arrows show where the measurements for the position of the soundpost were made using nearer surfaces.
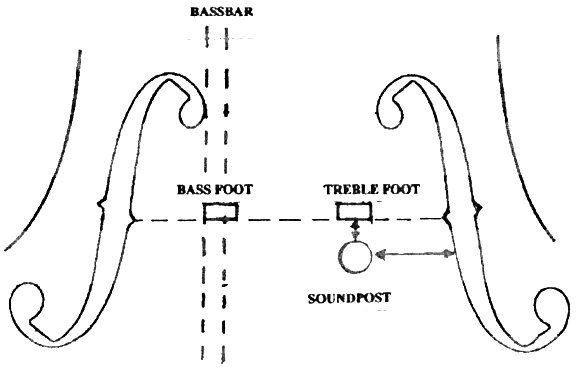Figure 1 Bridge and soundpost geometry showing the bridge line between the inner notches of the soundholes taken as the Stop, the position of the bridge feet and soundpost. The arrows indicate how the position of the soundpost was measured.
The position of the soundpost was measured from the nearer surfaces of the bridge and the soundpost, as show in figure 1. The soundpost was always placed 5 mm from the line of the rear face of the bridge. The horizontal position was measured from the inner edge of the treble soundhole. Two positions were used, one inside the treble foot of the bridge and one outside. For the soundpost (54 mm long and 6.4 mm dia.) which was placed inside the treble foot, the distance was 30 mm from the soundhole using nearer surfaces, as stated. The soundpost (52.5 mm long and 6.4 mm dia.) outside the treble foot position was 17 mm from the soundhole. Located at the treble foot, the soundpost would have been 22 mm from the soundhole. If we use centrelines for the soundpost and the treble foot, the soundpost, when it was 30 mm from the soundhole (inner surfaces) was 8 mm inside the treble foot (centre to centre); the soundpost when outside the treble foot was 5 mm outside, using centres. To place these positions in context, the distance between the bridge feet was 30 mm using centrelines. The centreline of the violin was 40 mm from the treble soundhole.
Top plate stiffness at the bridge feet as a function of soundpost position.
The effect of the position of the soundpost for this violin on the stiffness at the two bridge feet positions of the top plate were studied with the bridge removed, as explained in my thesis [1]. An extended series of measurements on this violin is shown in figure 2 for this violin. It can be seen that the stiffnesses at positions measured from the soundhole suggest, for this violin, that the stiffness at the treble foot position is above that at the bass foot position when the soundpost is outside the treble foot. When the soundpost is inside the treble foot, the stiffness at the treble foot position is below that at the bass foot position. This is illustrated in figure 2. The stiffness at the bass foot remains constant. Other violins have not shown this effect as clearly. Distance from treble soundhole (nearer surfaces). T/F = position of treble foot, in mm.
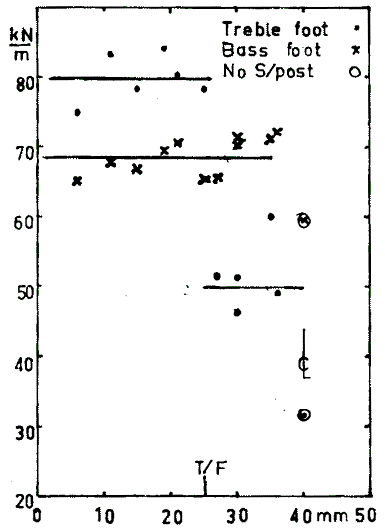 Figure 2 Stiffness at the bridge foot positions as the soundpost is moved in from the treble soundhole.
The relative stiffnesses for the three conditions ([1] p 165) for this violin, expressed as a ratio of the stiffness, in kN/m, at the treble foot over that at the bass foot were: no soundpost 30/60; soundpost at 5/30; 55/70 and soundpost at 5/17; 80/70. For the favourable position the stiffness at the treble foot was greater than at the bass foot while for the other positions the stiffness at the treble foot was lower, about half for no soundpost.
|
Tap response
The violin, with strings damped, was suspended vertically in a frame using rubber bands and the tap response determined with an impact bar, 13.2 g, at the top edge of the bridge on the treble side. The tap response for the three conditions was recorded with a microphone at 100 mm in front of the violin. In addition, a second response was taken by placing a magnet, 0.15 g, at the top edge on the bass side of the bridge, a coil picking up the motion of the magnet. The results are shown in figures 3 and 4.
Figure 3 Tap response with microphone for: Top; No soundpost. Centre; Soundpost at 5/30. Bottom; Soundpost at 5/17.
Figure 4 Tap response with magnet/coil for: Top; No soundpost. Centre; Soundpost at 5/30. Bottom; Soundpost at 5/17.
Peak frequencies as a function of soundpost position
The prominent peaks for the three conditions are shown in table 1 for the microphone pickup and in table 2 for the magnet/coil.
Table 1 Mode frequencies (Hz) for prominent peaks recorded by microphone.
| Mode |
A0 |
C2 |
B1- |
B1+ |
|
|
|
|
| No soundpost |
253 |
382 |
? |
470? |
560 |
- |
- |
1184 |
| Soundpost at 5/30 |
285 |
- |
436 |
468 |
560 |
840 |
- |
1184 |
| Soundpost at 5/17 |
280 |
398 |
447 |
474 |
565 |
840 |
947 |
1195 |
The peaks had different profiles for the conditions with and without a soundpost. The response fell off from about 3 kHz. With the soundpost inside the bridge foot, the modes at about 500 Hz were poorly defined but the falloff did not occur till about 4 kHz. With the soundpost outside the bridge foot, the modes at 500 Hz were well defined and the falloff was similar from about 4 kHz. Modes A1 and C2 were not prominent.
Table 2 Mode frequencies (Hz) for prominent peaks recorded by magnet/coil.
| Mode |
A0 |
A(H) |
C2 |
B1- |
A1 |
B1+ |
|
|
|
| No soundpost |
- |
242? |
- |
- |
- |
511 |
770 |
921 |
|
| Soundpost at 5/30 |
285 |
291 |
- |
- |
- |
554 |
786 |
921 |
1184 |
| Soundpost at 5/17 |
280 |
291 |
431 |
447 |
474 |
565 |
840 |
953 |
1211 |
The peaks recorded in table 2 include those that do not contribute to sound production. The mode A(H) is the Helmholtz resonance associated with A0. For no soundpost A0 does not appear in this plot. For this condition and the soundpost at 5/30, the lower body peaks do not appear, only B1+.
Sound samples
The sound samples for the three soundpost conditions were recorded as .wav files and are available below.
 No sound post
Sound post at 5/17 position
Sound post at 5/30 position
The Long Time Average Spectra, LTAS, for these files are shown in figures 5 and 6. The comparison is made between the soundpost position at 5/17 and the other two in turn. The main differences occur in the frequency range below 2 kHz. The plot for no soundpost appears below that for the 5/17 position.
With the soundpost inside the treble foot of the bridge, regarded as a poor position, the discrepancy between the two plots occurs over the full range to 5 kHz. The curve for 5/30 lies mostly below that for 5/17 but there is a region at 4.5 to 5 kHz where it lies above, suggesting the possibility of harshness in the sound.
Discussion
The stiffnesses at the bridge feet positions was mentioned briefly earlier. This might have a bearing on the interpretation of the result so some discussion is given here. The static stiffness (measured by direct loading at the bridge foot position with strings relaxed and no bridge in place) showed that, at the bass foot position, the stiffness was 70 kN/m, for all positions of the soundpost. At the treble foot position, the stiffness depended on whether the soundpost was outside or inside the bridge foot. With the soundpost outside the treble bridge foot position, the stiffness at the bridge foot position was about 10 kN/m higher than at the bass foot position. With the soundpost inside the bridge foot position, the stiffness was about 20 kN/m lower at the treble foot position than at the bass foot position.
With no soundpost in place the stiffness at the bass foot position was 60 kN/m and at the treble foot position it was 30 kN/m. The presence of the soundpost has an effect on the stiffness at the bass foot position.
All the preceding values were measured on a particular instrument, called violin No 2 in the thesis. This violin has a top plate about 2.9 mm thick in the region of the bridge with a normal arch shape 15 mm high. The stiffness at the bridge feet will vary with arch type, plate thickness, bassbar stiffness as well as other structural variations in the bridge region of the top. The position of the soundpost will have an influence on the size of a small area, called the 'island', of the top plate that is out of phase with the top generally but in phase with the back plate i.e. its size and position, described by Cremer [2]. It will also influence the pivot point for the rocking motion of the bridge. Placed between the feet, the soundpost could well be the pivot point. Outside the treble foot, the soundpost will be in the 'island' and act to transmit motion to the back.
Conclusion
The three distinct positions of the soundpost studied in this experiment have shown quite different behaviour in the tap response and LTAS. The relative stiffness felt by the two bridge feet as determined by the bassbar and plate properties on the response and sound quality requires further study.
References
Acknowledgments
I am indebted to Peter Coombes for composing and playing the musical fragment that appears in this paper and to Professor Joe Wolfe for the LTAS plots.
|
